Concentration de l'attention :

Définition. Une fonction l'espèce est appelée fonction exponentielle .

Commenter. Exclusion de base une nombres 0 ; 1 et valeurs négatives une expliqué par les circonstances suivantes :

L'expression analytique elle-même un x dans ces cas, il garde son sens et peut être rencontré dans la résolution de problèmes. Par exemple, pour l'expression x y point x = 1 ; y = 1 entre dans la plage des valeurs acceptables.

Construire des graphes de fonctions : et .

Graphique d'une fonction exponentielle
y= une X, un > 1	y= une X , 0< a < 1

Propriétés de la fonction exponentielle

Propriétés de la fonction exponentielle	y= une X, un > 1	y= une X , 0< a < 1
Portée de la fonction
2. Plage de valeurs de fonction
3. Intervalles de comparaison avec l'unité	à X> 0, un X > 1	à X > 0, 0< a X < 1
	à X < 0, 0< a X < 1	à X < 0, a X > 1
4. Pair, impair.	La fonction n'est ni paire ni impaire (fonction générale).
5. Monotonie.	augmente de façon monotone de R	diminue de façon monotone de R
6. Extrêmes.	Fonction exponentielle n'a pas d'extrêmes.
7.Asymptote	Axe O X est une asymptote horizontale.
8. Pour toutes les valeurs réelles X Et y;

Lorsque le tableau est rempli, les tâches sont résolues en parallèle avec le remplissage.

Tâche numéro 1. (Pour trouver le domaine de la fonction).

Quelles valeurs d'argument sont valides pour les fonctions :

Tâche numéro 2. (Pour trouver la portée de la fonction).

La figure montre un graphique d'une fonction. Spécifiez la portée et la portée de la fonction :

Tâche numéro 3. (Pour indiquer les intervalles de comparaison avec l'unité).

Comparez chacune des puissances suivantes avec une :

Tâche numéro 4. (Pour étudier la fonction de monotonie).

Comparer les nombres réels par magnitude m Et n si:

Tâche numéro 5. (Pour étudier la fonction de monotonie).

Faire une conclusion sur la base une, si:

y(x) = 10x ; f(x) = 6x ; z(x) - 4x

Comment sont les graphiques des fonctions exponentielles les uns par rapport aux autres pour x > 0, x = 0, x< 0?

Dans un plan de coordonnées, des graphiques de fonctions sont tracés :

y(x) = (0,1) x ; f(x) = (0.5)x ; z(x) = (0,8) x .

Comment sont les graphiques des fonctions exponentielles les uns par rapport aux autres pour x > 0, x = 0, x< 0?

Nombre l'une des constantes les plus importantes en mathématiques. Par définition, il égal à la limite de la suite avec illimité croissant n . La désignation e introduit Léonhard Euler en 1736. Il a calculé les 23 premiers chiffres de ce nombre en notation décimale, et le nombre lui-même a été nommé d'après Napier "le nombre non pair". Nombre e joue un rôle particulier dans l'analyse mathématique. Fonction exponentielle avec socle e, appelé l'exposant et noté y = e x. Premiers signes Nombres e facile à retenir: deux, une virgule, sept, l'année de naissance de Léon Tolstoï - deux fois, quarante-cinq, quatre-vingt-dix, quarante-cinq.

Devoirs:

Kolmogorov page 35 ; n° 445-447 ; 451 ; 453.

Répétez l'algorithme pour construire des graphes de fonctions contenant une variable sous le signe du module.

Fonction exponentielle

Fonction de la forme y = a X , où a est supérieur à zéro et a n'est pas égal à un est appelée une fonction exponentielle. Les principales propriétés de la fonction exponentielle :

1. Le domaine de la fonction exponentielle sera l'ensemble des nombres réels.

2. La plage de la fonction exponentielle sera l'ensemble de tous les nombres réels positifs. Parfois, cet ensemble est noté R+ par souci de brièveté.

3. Si dans une fonction exponentielle la base a est supérieure à un, alors la fonction sera croissante sur tout le domaine de définition. Si la fonction exponentielle de la base a satisfait la condition suivante 0

4. Toutes les propriétés de base des degrés seront valides. Les principales propriétés des degrés sont représentées par les égalités suivantes :

une X *une y = un (x+y) ;

(une X )/(une y ) = un (x-y) ;

(un B) X = (un X )*(une y );

(un B) X = un X /b X ;

(une X ) y = un (x*y) .

Ces égalités seront valables pour toutes les valeurs réelles de x et y.

5. Le graphique de la fonction exponentielle passe toujours par le point de coordonnées (0;1)

6. Selon que la fonction exponentielle augmente ou diminue, son graphique aura l'un des deux types.

La figure suivante montre un graphique d'une fonction exponentielle croissante : a>0.

La figure suivante est un graphique d'une fonction exponentielle décroissante : 0

Le graphique de la fonction exponentielle croissante et le graphique de la fonction exponentielle décroissante, selon la propriété décrite au cinquième paragraphe, passent par le point (0 ; 1).

7. Une fonction exponentielle n'a pas de points extrêmes, c'est-à-dire qu'elle n'a pas de points minimum et maximum de la fonction. Si nous considérons la fonction sur un segment particulier, alors la fonction prendra les valeurs minimale et maximale aux extrémités de cet intervalle.

8. La fonction n'est ni paire ni impaire. Une fonction exponentielle est une fonction générale. Cela se voit également sur les graphiques, aucun d'entre eux n'est symétrique ni par rapport à l'axe Oy ni par rapport à l'origine.

Logarithme

Les logarithmes ont toujours été considérés sujet difficile en mathématiques scolaires. Il existe de nombreuses définitions différentes du logarithme, mais pour une raison quelconque, la plupart des manuels utilisent la plus complexe et la plus malheureuse d'entre elles.

Nous allons définir le logarithme simplement et clairement. Créons un tableau pour cela :

Donc, nous avons des puissances de deux. Si vous prenez le nombre de la ligne du bas, vous pouvez facilement trouver la puissance à laquelle vous devez élever un deux pour obtenir ce nombre. Par exemple, pour obtenir 16, vous devez élever deux à la puissance quatre. Et pour obtenir 64, vous devez élever deux à la sixième puissance. Cela se voit sur le tableau.

Et maintenant - en fait, la définition du logarithme :

Définition

Logarithme base a à partir de l'argument x est la puissance à laquelle le nombre doit être élevé une pour obtenir le numéro X.

La désignation

log a x = b
où a est la base, x est l'argument, b Quel est exactement le logarithme.

Par exemple, 2 3 = 8 ⇒ log 2 8 = 3 (le logarithme en base 2 de 8 est trois car 2 3 = 8). Autant enregistrer 2 64 = 6, puisque 2 6 = 64.

L'opération consistant à trouver le logarithme d'un nombre dans une base donnée s'appellelogarithme . Ajoutons donc une nouvelle ligne à notre tableau :

Malheureusement, tous les logarithmes ne sont pas considérés aussi facilement. Par exemple, essayez de trouver log 2 5. Le nombre 5 n'est pas dans le tableau, mais la logique veut que le logarithme se situe quelque part sur l'intervalle. Parce que 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

De tels nombres sont appelés irrationnels : les nombres après la virgule décimale peuvent être écrits indéfiniment, et ils ne se répètent jamais. Si le logarithme s'avère irrationnel, il vaut mieux le laisser ainsi : log 2 5, log 3 8, log 5 100.

Il est important de comprendre que le logarithme est une expression à deux variables (base et argument). Au début, beaucoup de gens confondent où se trouve la base et où se trouve l'argument. Pour éviter les malentendus gênants, il suffit de regarder l'image :

Devant nous n'est rien de plus que la définition du logarithme. Rappel : le logarithme est une puissance , auquel vous devez élever la base pour obtenir l'argument. C'est la base qui est élevée à une puissance - sur l'image, elle est surlignée en rouge. Il s'avère que la base est toujours en bas ! Je dis cette merveilleuse règle à mes élèves dès la première leçon - et il n'y a pas de confusion.

Nous avons compris la définition - il reste à apprendre à compter les logarithmes, c'est-à-dire débarrassez-vous du signe "log". Pour commencer, notons que Deux faits importants découlent de la définition :

L'argument et la base doivent toujours être supérieurs à zéro. Cela découle de la définition du degré par un exposant rationnel, à laquelle se réduit la définition du logarithme.

La base doit être différente de l'unité, car une unité pour n'importe quelle puissance est toujours une unité. De ce fait, la question « à quelle puissance faut-il élever un pour en avoir deux » n'a pas de sens. Un tel diplôme n'existe pas !

De telles restrictions appelé Plage valide(ODZ). Il s'avère que l'ODZ du logarithme ressemble à ceci : log une X = b ⇒ x > 0, a > 0, a ≠ 1.

Remarquerez que pas de limite de nombre b (valeur logarithmique) ne se chevauchent pas. Par exemple, le logarithme peut très bien être négatif : log 2 0,5 = −1, car 0,5 = 2 −1 .

Cependant, nous ne considérons maintenant que les expressions numériques, où il n'est pas nécessaire de connaître l'ODZ du logarithme. Toutes les restrictions ont déjà été prises en compte par les compilateurs des problèmes. Mais lorsque les équations logarithmiques et les inégalités entreront en jeu, les exigences du DHS deviendront obligatoires. En effet, dans la base et l'argumentation il peut y avoir des constructions très fortes qui ne correspondent pas forcément aux restrictions ci-dessus.

À présent considérer le général schéma de calcul des logarithmes. Il se compose de trois étapes :

Soumettre Fondation a et argument x sous la forme d'un diplôme avec un minimum base possible, grandes unités. En cours de route, il vaut mieux se débarrasser des fractions décimales ;

Choisissez une variable b équation : x = a b ;

Numéro reçu b sera la réponse.

C'est tout! Si le logarithme s'avère irrationnel, cela se verra déjà à la première étape. L'exigence que la base soit supérieure à un est très pertinente : cela réduit le risque d'erreur et simplifie grandement les calculs. Semblable à décimales: si vous les traduisez immédiatement en ordinaires, il y aura beaucoup moins d'erreurs.

Voyons comment ce schéma fonctionne sur exemples concrets:

Calculer le logarithme : log 5 25

Représentons la base et l'argument sous la forme d'une puissance de cinq : 5 = 5 1 ; 25 = 52 ;

Faisons et résolvons l'équation :
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;

Réponse reçue : 2.

Calculez le logarithme :

Représentons la base et l'argument comme une puissance de trois : 3 = 3 1 ; 1/81 \u003d 81 -1 \u003d (3 4) -1 \u003d 3 -4;

Faisons et résolvons l'équation :

J'ai la réponse : -4.

−4

Calculer le logarithme : log 4 64

Représentons la base et l'argument comme une puissance de deux : 4 = 2 2 ; 64 = 26 ;

Faisons et résolvons l'équation :
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ;

Réponse reçue : 3.

Calculer le logarithme : log 16 1

Représentons la base et l'argument comme une puissance de deux : 16 = 2 4 ; 1 = 20 ;

Faisons et résolvons l'équation :
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ;

Réponse reçue : 0.

Calculer le logarithme : log 7 14

Représentons la base et l'argument comme une puissance de sept : 7 = 7 1 ; 14 n'est pas représenté comme une puissance de sept, car 7 1< 14 < 7 2 ;

Il résulte du paragraphe précédent que le logarithme n'est pas considéré ;

La réponse est inchangée : log 7 14.

journal 7 14

Une petite note sur le dernier exemple. Comment s'assurer qu'un nombre n'est pas une puissance exacte d'un autre nombre ? Très simple - il suffit de le décomposer en facteurs premiers. S'il y a au moins deux facteurs distincts dans l'expansion, le nombre n'est pas une puissance exacte.

Découvrez si les puissances exactes du nombre sont : 8 ; 48 ; 81 ; 35; Quatorze.

8 \u003d 2 2 2 \u003d 2 3 - le degré exact, car il n'y a qu'un seul multiplicateur ;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 n'est pas une puissance exacte car il y a deux facteurs : 3 et 2 ;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - degré exact;
35 = 7 5 - encore une fois pas un degré exact ;
14 \u003d 7 2 - encore une fois pas un degré exact;

8, 81 - degré exact ; 48, 35, 14 - non.

Notez également que les nombres premiers eux-mêmes sont toujours des puissances exactes d'eux-mêmes.

Logarithme décimal

Certains logarithmes sont si courants qu'ils ont un nom et une désignation spéciaux.

Définition

Logarithme décimalà partir de l'argument x est le logarithme en base 10, soit la puissance à laquelle vous devez élever le nombre 10 pour obtenir le nombre X.

La désignation

lgx

Par exemple, log 10 = 1 ; log 100 = 2 ; lg 1000 = 3 - etc.

À partir de maintenant, lorsqu'une phrase comme "Find lg 0.01" apparaît dans le manuel, sachez qu'il ne s'agit pas d'une faute de frappe. C'est le logarithme décimal. Cependant, si vous n'êtes pas habitué à une telle désignation, vous pouvez toujours la réécrire :
log x = log 10 x

Tout ce qui est vrai pour les logarithmes ordinaires est également vrai pour les décimaux.

un algorithme naturel

Il existe un autre logarithme qui a sa propre notation. En un sens, il est encore plus important que le nombre décimal. Il s'agit de sur le logarithme naturel.

Définition

un algorithme naturelà partir de l'argument x est le logarithme de base e , c'est à dire. la puissance à laquelle le nombre doit être élevé e pour obtenir le numéro X.

La désignation

en x

Beaucoup se demanderont : quel est le nombre e ? C'est un nombre irrationnel, sa valeur exacte ne peut pas être trouvée et écrite. Voici juste les premiers chiffres :
e = 2,718281828459...

Nous n'approfondirons pas ce qu'est ce nombre et pourquoi il est nécessaire. N'oubliez pas que e est la base du logarithme naturel :
dans x = log e x

Ainsi ln e = 1; log e 2 = 2; En e 16 = 16 - etc... Par contre, ln 2 est un nombre irrationnel. En général, le logarithme naturel de tout nombre rationnel est irrationnel. Sauf, bien sûr, l'unité : ln 1 = 0.

Pour les logarithmes naturels, toutes les règles valables pour les logarithmes ordinaires sont valables.

Propriétés de base des logarithmes

Les logarithmes, comme n'importe quel nombre, peuvent être additionnés, soustraits et convertis de toutes les manières possibles. Mais comme les logarithmes ne sont pas des nombres tout à fait ordinaires, il existe ici des règles appelées propriétés de base.

Ces règles doivent être connues - aucun problème logarithmique sérieux ne peut être résolu sans elles. De plus, il y en a très peu - tout peut être appris en une journée. Alors, commençons.

Addition et soustraction de logarithmes

Considérons deux logarithmes de même base : log a x et log a y . Ensuite, ils peuvent être ajoutés et soustraits, et :

Journal un x +journal un y = journal une ( X · y );

Journal un x −journal un y = journal une ( X : y ).

Alors, la somme des logarithmes est égale au logarithme du produit, et la différence est le logarithme du quotient. Attention : le point clé ici, ce sont les mêmes bases. Si les bases sont différentes, ces règles ne fonctionnent pas !

Ces formules aideront à calculer l'expression logarithmique même lorsque ses parties individuelles ne sont pas prises en compte (voir la leçon " "). Jetez un oeil aux exemples - et voyez:

Trouvez la valeur de l'expression : log 6 4 + log 6 9.

Puisque les bases des logarithmes sont les mêmes, nous utilisons la formule de somme :
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Trouvez la valeur de l'expression : log 2 48 − log 2 3.

Les bases sont les mêmes, on utilise la formule de différence :
bûche 2 48 - bûche 2 3 = bûche 2 (48 : 3) = bûche 2 16 = 4.

Trouvez la valeur de l'expression : log 3 135 − log 3 5.

Encore une fois, les bases sont les mêmes, nous avons donc :
log 3 135 − log 3 5 = log 3 (135 : 5) = log 3 27 = 3.

Comme vous pouvez le voir, les expressions originales sont constituées de "mauvais" logarithmes, qui ne sont pas considérés séparément. Mais après les transformations, des nombres tout à fait normaux se révèlent. Sur la base de ce fait, de nombreux papiers de test. Oui, ce contrôle - des expressions similaires en toute sincérité (parfois - avec pratiquement aucun changement) sont proposés à l'examen.

Suppression de l'exposant du logarithme

Maintenant, compliquons un peu la tâche. Et s'il y a un degré dans la base ou l'argument du logarithme ? Puis l'exposant de ce degré peut être extrait du signe du logarithme selon les règles suivantes :

Il est facile de voir que dernière règle suit les deux premiers. Mais il vaut mieux s'en souvenir quand même - dans certains cas, cela réduira considérablement la quantité de calculs.

Bien sûr toutes ces règles ont un sens si le logarithme ODZ est respecté : une > 0, une ≠ 1, x > 0 vous pouvez entrer les nombres avant le signe du logarithme dans le logarithme lui-même. C'est ce qui est le plus souvent demandé.

Trouvez la valeur de l'expression : log 7 49 6 .

Débarrassons-nous du degré dans l'argument selon la première formule :
bûche 7 49 6 = 6 bûche 7 49 = 6 2 = 12

Trouvez la valeur de l'expression :

Notez que le dénominateur est un logarithme dont la base et l'argument sont des puissances exactes : 16 = 2 4 ; 49 = 72. Nous avons:

Je pense que le dernier exemple mérite d'être clarifié. Où sont passés les logarithmes ? Jusqu'au tout dernier moment, nous ne travaillons qu'avec le dénominateur. Ils ont présenté la base et l'argument du logarithme sous forme de degrés et ont sorti les indicateurs - ils ont obtenu une fraction «à trois étages».

Regardons maintenant la fraction principale. Le numérateur et le dénominateur ont le même nombre : log 2 7. Puisque log 2 7 ≠ 0, on peut réduire la fraction - 2/4 restera au dénominateur. Selon les règles de l'arithmétique, les quatre peuvent être transférés au numérateur, ce qui a été fait. Le résultat est la réponse : 2.

Transition vers une nouvelle fondation

Parlant des règles d'addition et de soustraction de logarithmes, j'ai spécifiquement souligné qu'elles ne fonctionnent qu'avec les mêmes bases. Et si les bases sont différentes ? Et si ce ne sont pas des puissances exactes du même nombre ?

Les formules de transition vers une nouvelle base viennent à la rescousse. Nous les formulons sous la forme d'un théorème :

Théorème

Laissez le logarithme log un x . Alors pour n'importe quel nombre c tel que c > 0 et c ≠ 1, l'égalité est vraie :

En particulier, si l'on pose c = x, on obtient :

Il résulte de la deuxième formule qu'il est possible d'intervertir la base et l'argument du logarithme, mais dans ce cas l'expression entière est « retournée », c'est-à-dire le logarithme est au dénominateur.

Ces formules se retrouvent rarement dans les expressions numériques ordinaires. Il est possible d'évaluer à quel point ils sont pratiques uniquement lors de la résolution d'équations et d'inéquations logarithmiques.

Cependant, il y a des tâches qui ne peuvent être résolues qu'en passant à une nouvelle fondation. Considérons quelques-uns de ceux-ci :

Trouvez la valeur de l'expression : log 5 16 log 2 25.

Notez que les arguments des deux logarithmes sont des exposants exacts. Retirons les indicateurs : log 5 16 = log 5 2 4 = 4log 5 2 ; log 2 25 = log 2 5 2 = 2 log 2 5 ;

Inversons maintenant le deuxième logarithme :

Étant donné que le produit ne change pas à partir de la permutation des facteurs, nous avons multiplié calmement quatre et deux, puis avons calculé les logarithmes.

Trouver la valeur de l'expression : log 9 100 lg 3.

La base et l'argument du premier logarithme sont des puissances exactes. Écrivons-le et débarrassons-nous des indicateurs:

Débarrassons-nous maintenant du logarithme décimal en passant à une nouvelle base :

Identité logarithmique de base

Souvent, dans le processus de résolution, il est nécessaire de représenter un nombre sous forme de logarithme par rapport à une base donnée. Dans ce cas, les formules nous aideront :

Dans le premier cas, le nombre n devient l'exposant de l'argument. Nombre n peut être absolument n'importe quoi, car c'est juste la valeur du logarithme.

La deuxième formule est en fait une définition paraphrasée. Ça s'appelle comme ça :identité logarithmique de base.

En effet, que se passera-t-il si le nombre b est élevé à une puissance telle que le nombre b à cette puissance donne le nombre a ? C'est vrai : c'est le même nombre a. Relisez attentivement ce paragraphe - beaucoup de gens "s'y accrochent".

Comme les nouvelles formules de conversion de base, l'identité logarithmique de base est parfois la seule solution possible.

Une tâche

Trouvez la valeur de l'expression :

Solution

Notez que log 25 64 = log 5 8 - vient de sortir le carré de la base et l'argument du logarithme. Etant donné les règles de multiplication des puissances de même base, on obtient :

200

Si quelqu'un n'est pas au courant, c'était une vraie tâche de l'examen :)

Unité logarithmique et zéro logarithmique

En conclusion, je donnerai deux identités qu'il est difficile d'appeler des propriétés - ce sont plutôt des conséquences de la définition du logarithme. Ils se retrouvent constamment dans les problèmes et, étonnamment, créent des problèmes même pour les étudiants "avancés".

log a a = 1 est unité logarithmique. Rappelez-vous une fois pour toutes : le logarithme de n'importe quelle base une de cette base elle-même est égale à un.

log un 1 = 0 est zéro logarithmique. Base un peut être n'importe quoi, mais si l'argument est un - le logarithme est zéro ! car un 0 = 1 est une conséquence directe de la définition.

C'est toutes les propriétés. Assurez-vous de vous entraîner à les mettre en pratique !

Cours #2

Sujet : Une fonction exponentielle, ses propriétés et son graphique.

Cible: Vérifier la qualité d'assimilation de la notion de « fonction exponentielle » ; former des compétences à reconnaître une fonction exponentielle, à utiliser ses propriétés et ses graphiques, à apprendre aux étudiants à utiliser les formes analytiques et graphiques d'enregistrement d'une fonction exponentielle; offrir un environnement de travail en classe.

Équipement: tableau, affiches

Formulaire de leçon: Salle de classe

Type de leçon: cours pratique

Type de leçon: leçon de formation professionnelle

Plan de cours

1. Moment organisationnel

2. Travail indépendant et vérification devoirs

3. Résolution de problèmes

4. Résumé

5. Devoirs

Pendant les cours.

1. Moment organisationnel :

Salut. Ouvrez les cahiers, notez la date d'aujourd'hui et le sujet de la leçon "Fonction exponentielle". Aujourd'hui, nous allons continuer à étudier la fonction exponentielle, ses propriétés et son graphique.

2. Travail indépendant et vérification des devoirs .

Cible: vérifier la qualité d'assimilation de la notion de "fonction exponentielle" et vérifier la réalisation de la partie théorique du devoir

Méthode: tâche de test, enquête frontale

Comme devoir, on vous a donné des numéros du cahier de problèmes et un paragraphe du manuel. Nous ne vérifierons pas l'exécution des nombres du manuel maintenant, mais vous remettrez vos cahiers à la fin de la leçon. Maintenant, la théorie va être testée sous la forme d'un petit test. La tâche est la même pour tout le monde : on vous donne une liste de fonctions, vous devez savoir lesquelles d'entre elles sont indicatives (soulignez-les). Et à côté de la fonction exponentielle, vous devez écrire si elle augmente ou diminue.

Option 1 Répondre B) D) - exponentielle, décroissante	Option 2 Répondre D) - exponentielle, décroissante RÉ) - indicatif, croissant
Variante 3 Répondre MAIS) - indicatif, croissant B) - exponentielle, décroissante	Variante 4 Répondre MAIS) - exponentielle, décroissante DANS) - indicatif, croissant

Rappelons maintenant ensemble quelle fonction est appelée exponentielle ?

Une fonction de la forme , où et , est appelée une fonction exponentielle.

Quelle est la portée de cette fonction ?

Tous les nombres réels.

Quelle est la plage de la fonction exponentielle ?

Tous les nombres réels positifs.

Diminue si la base est supérieure à zéro mais inférieure à un.

Quand une fonction exponentielle décroît-elle sur son domaine ?

Augmente si la base est supérieure à un.

3. Résolution de problèmes

Cible: former des compétences à la reconnaissance d'une fonction exponentielle, à l'utilisation de ses propriétés et de ses graphiques, apprendre aux étudiants à utiliser les formes analytiques et graphiques d'enregistrement d'une fonction exponentielle

Méthode: démonstration par l'enseignant de la résolution de problèmes types, travail oral, travail au tableau, travail dans un cahier, conversation de l'enseignant avec les élèves.

Les propriétés de la fonction exponentielle peuvent être utilisées lors de la comparaison de 2 nombres ou plus. Par exemple : N° 000. Comparez les valeurs et si a) ..gif" width="37" height="20 src=">, alors c'est un travail assez délicat : il faudrait prendre la racine cubique de 3 et 9, et les comparer. Mais on sait que ça augmente, ça est dans sa propre file d'attente signifie que lorsque l'argument augmente, la valeur de la fonction augmente, c'est-à-dire qu'il nous suffit de comparer les valeurs de l'argument entre elles et, évidemment, que (peut être démontré sur une affiche avec une fonction exponentielle croissante). Et toujours lors de la résolution de tels exemples, déterminez d'abord la base de la fonction exponentielle, comparez avec 1, déterminez la monotonie et procédez à la comparaison des arguments. Dans le cas d'une fonction décroissante : à mesure que l'argument augmente, la valeur de la fonction diminue, donc le signe de l'inégalité change lorsque l'on passe de l'inégalité des arguments à l'inégalité des fonctions. Puis on résout oralement : b)

-

DANS)

-

G)

-

- N° 000. Comparez les chiffres : a) et

La fonction est donc croissante, alors

Pourquoi ?

Augmenter la fonction et

Donc la fonction est décroissante, alors

Les deux fonctions augmentent sur tout leur domaine de définition, puisqu'elles sont exponentielles de base supérieure à un.

Quel est le sens de cela?

Nous construisons des graphiques :

Quelle fonction se développe plus rapidement lors de l'effort https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">

Quelle fonction diminue plus rapidement lors de l'effort https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">

Sur l'intervalle, laquelle des fonctions a la plus grande valeur en un point particulier ?

D), https://pandia.ru/text/80/379/images/image068_0.gif" width="69" height="57 src=">. Tout d'abord, découvrons la portée de ces fonctions. Est-ce qu'elles coïncider?

Oui, le domaine de ces fonctions est tous les nombres réels.

Nommez la portée de chacune de ces fonctions.

Les plages de ces fonctions coïncident : tous les nombres réels positifs.

Déterminer le type de monotonie de chacune des fonctions.

Les trois fonctions décroissent sur tout leur domaine de définition, puisqu'elles sont exponentielles avec une base inférieure à un et supérieure à zéro.

Quel est le point singulier du graphique d'une fonction exponentielle ?

Quel est le sens de cela?

Quelle que soit la base du degré d'une fonction exponentielle, si l'exposant est 0, alors la valeur de cette fonction est 1.

Nous construisons des graphiques :

Analysons les graphiques. Combien de points d'intersection les graphes de fonctions ont-ils ?

Quelle fonction diminue plus rapidement lors de l'effort ? https://pandia.ru/text/80/379/images/image070.gif

Quelle fonction se développe plus rapidement lorsque vous vous efforcez ? https://pandia.ru/text/80/379/images/image070.gif

Sur l'intervalle, laquelle des fonctions a la plus grande valeur en un point particulier ?

Sur l'intervalle, laquelle des fonctions a la plus grande valeur en un point particulier ?

Pourquoi les fonctions exponentielles de bases différentes n'ont-elles qu'un seul point d'intersection ?

Les fonctions exponentielles sont strictement monotones sur tout leur domaine de définition, elles ne peuvent donc se croiser qu'en un point.

La tâche suivante se concentrera sur l'utilisation de cette propriété. № 000. Trouver la plus grande et la plus petite valeur d'une fonction donnée sur un intervalle donné a). Rappelons qu'une fonction strictement monotone prend ses valeurs minimale et maximale aux extrémités d'un intervalle donné. Et si la fonction est croissante, alors son valeur la plus élevée sera à l'extrémité droite du segment, et le plus petit à l'extrémité gauche du segment (démonstration sur l'affiche, en utilisant la fonction exponentielle comme exemple). Si la fonction est décroissante, alors sa plus grande valeur sera à l'extrémité gauche du segment, et la plus petite à l'extrémité droite du segment (démonstration sur l'affiche, en utilisant la fonction exponentielle comme exemple). La fonction augmente, car, par conséquent, la plus petite valeur de la fonction sera au point https://pandia.ru/text/80/379/images/image075_0.gif" width="145" height="29" > Points b ) , dans) d) résoudre des cahiers par vous-même, nous le vérifierons oralement.

Les élèves résolvent le problème dans leur cahier

Fonction décroissante

Fonction décroissante la plus grande valeur de la fonction sur l'intervalle la plus petite valeur de la fonction sur le segment

Fonction croissante la plus petite valeur de la fonction sur le segment la plus grande valeur de la fonction sur l'intervalle

- № 000. Trouver la plus grande et la plus petite valeur d'une fonction donnée sur un intervalle donné a) . Cette tâche est presque la même que la précédente. Mais ici on ne donne pas un segment, mais un rayon. Nous savons que la fonction augmente et qu'elle n'a ni la plus grande ni la plus petite valeur sur toute la droite numérique https://pandia.ru/text/80/379/images/image063_0.gif" width="68" height = "20">, et tend vers en , c'est-à-dire que sur le rayon, la fonction en tend vers 0, mais n'a pas sa propre la plus petite valeur, mais il a la plus grande valeur au point . b) , dans) , G) Résolvez vos propres cahiers, nous le vérifierons oralement.

Nous introduisons d'abord la définition d'une fonction exponentielle.

La fonction exponentielle $f\left(x\right)=a^x$, où $a >1$.

Introduisons les propriétés de la fonction exponentielle, pour $a >1$.

\ \[pas de racine\] \

Intersection avec axes de coordonnées. La fonction ne coupe pas l'axe $Ox$, mais coupe l'axe $Oy$ au point $(0,1)$.

$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$

\ \[pas de racine\] \

Graphique (Fig. 1).

Figure 1. Graphique de la fonction $f\left(x\right)=a^x,\ for \ a >1$.

La fonction exponentielle $f\left(x\right)=a^x$, où $0

Introduisons les propriétés de la fonction exponentielle, pour $0

Le domaine de définition est tous les nombres réels.

$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- la fonction n'est ni paire ni impaire.

$f(x)$ est continue sur tout le domaine de définition.

La plage de valeurs est l'intervalle $(0,+\infty)$.

$f"(x)=\left(a^x\right)"=a^xlna$

\ \[pas de racine\] \ \[pas de racine\] \

La fonction est convexe sur tout le domaine de définition.

Comportement aux extrémités de la portée :

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]

Graphique (Fig. 2).

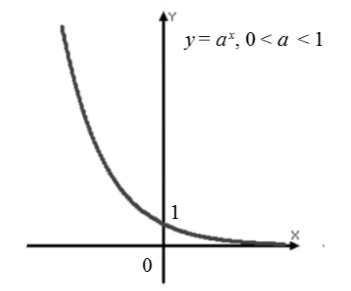
Un exemple de tâche pour construire une fonction exponentielle

Explorez et tracez la fonction $y=2^x+3$.

Solution.

Faisons une étude sur l'exemple du schéma ci-dessus:

Le domaine de définition est tous les nombres réels.

$f\left(-x\right)=2^(-x)+3$ -- la fonction n'est ni paire ni impaire.

$f(x)$ est continue sur tout le domaine de définition.

La plage de valeurs est l'intervalle $(3,+\infty)$.

$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$

La fonction croît sur tout le domaine de définition.

$f(x)\ge 0$ sur tout le domaine de définition.

Intersection avec axes de coordonnées. La fonction ne coupe pas l'axe $Ox$, mais coupe l'axe $Oy$ au point ($0,4)$

$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$

La fonction est convexe sur tout le domaine de définition.

Comportement aux extrémités de la portée :

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]

Graphique (Fig. 3).

Figure 3. Graphique de la fonction $f\left(x\right)=2^x+3$