Koncentrácia pozornosti:

Definícia. Funkcia druh sa nazýva exponenciálna funkcia .

Komentujte. Základné vylúčenie ačísla 0; 1 a záporné hodnoty a vysvetlené nasledujúcimi okolnosťami:

Samotný analytický výraz a x v týchto prípadoch si zachováva svoj význam a možno sa s ním stretnúť pri riešení problémov. Napríklad za výraz x y bodka x = 1; r = 1 sa dostane do rozsahu prijateľných hodnôt.

Zostrojte grafy funkcií: a .

Graf exponenciálnej funkcie
y= a X, a > 1	y= a X , 0< a < 1

Vlastnosti exponenciálnej funkcie

Vlastnosti exponenciálnej funkcie	y= a X, a > 1	y= a X , 0< a < 1
Rozsah funkcie
2. Rozsah funkčných hodnôt
3. Intervaly porovnávania s jednotkou	pri X> 0, a X > 1	pri X > 0, 0< a X < 1
	pri X < 0, 0< a X < 1	pri X < 0, a X > 1
4. Párne, nepárne.	Funkcia nie je párna ani nepárna (všeobecná funkcia).
5. Monotónnosť.	zvyšuje monotónne o R	klesá monotónne o R
6. Extrémy.	Exponenciálna funkcia nemá extrémy.
7.Asymptota	Os O X je horizontálna asymptota.
8. Pre akékoľvek skutočné hodnoty X a r;

Keď je tabuľka naplnená, paralelne s plnením sa riešia úlohy.

Úloha číslo 1. (Nájsť doménu funkcie).

Aké hodnoty argumentov sú platné pre funkcie:

Úloha číslo 2. (Zistiť rozsah funkcie).

Na obrázku je znázornený graf funkcie. Zadajte rozsah a rozsah funkcie:

Úloha číslo 3. (Určiť intervaly porovnávania s jednotkou).

Porovnajte každú z nasledujúcich mocností s jednou:

Úloha číslo 4. (Preštudovať funkciu pre monotónnosť).

Porovnajte skutočné čísla podľa veľkosti m a n ak:

Úloha číslo 5. (Preštudovať funkciu pre monotónnosť).

Urobte záver o základe a, ak:

y(x) = 10 x; f(x) = 6 x; z(x) - 4x

Ako sú grafy exponenciálnych funkcií voči sebe navzájom pre x > 0, x = 0, x< 0?

V jednej súradnicovej rovine sú vykreslené grafy funkcií:

y(x) = (0,1) x; f(x) = (0,5) x; z(x) = (0,8) x.

Ako sú grafy exponenciálnych funkcií voči sebe navzájom pre x > 0, x = 0, x< 0?

číslo jedna z najdôležitejších konštánt v matematike. Podľa definície to rovná limite postupnosti s neobmedzeným zvýšenie n . Označenie e zavedené Leonhard Euler v roku 1736. Vypočítal prvých 23 číslic tohto čísla v desiatkovom zápise a samotné číslo bolo pomenované po Napierovi „nerovesnícke číslo“. číslo e zohráva osobitnú úlohu v matematickej analýze. Exponenciálna funkcia so základňou e, nazývaný exponent a označené y = e x. Prvé známky čísla eľahko zapamätateľné: dva, čiarka, sedem, rok narodenia Leva Tolstého - dva krát, štyridsaťpäť, deväťdesiat, štyridsaťpäť.

Domáca úloha:

Kolmogorov s. 35; č. 445-447; 451; 453.

Zopakujte algoritmus na vytváranie grafov funkcií obsahujúcich premennú pod znakom modulu.

Exponenciálna funkcia

Funkcia tvaru y = a X , kde a je väčšie ako nula a a sa nerovná jednej, sa nazýva exponenciálna funkcia. Hlavné vlastnosti exponenciálnej funkcie:

1. Definičný obor exponenciálnej funkcie bude množina reálnych čísel.

2. Rozsah exponenciálnej funkcie bude množina všetkých kladných reálnych čísel. Niekedy sa táto množina pre stručnosť označuje ako R+.

3. Ak je v exponenciálnej funkcii základ a väčší ako jedna, potom funkcia bude narastať v celom definičnom obore. Ak exponenciálna funkcia pre základ a spĺňa nasledujúcu podmienku 0

4. Všetky základné vlastnosti stupňov budú platné. Hlavné vlastnosti stupňov sú reprezentované nasledujúcimi rovnosťami:

a X *a r = a (x+y) ;

(a X )/(a r ) = a (x-y) ;

(a*b) X = (a X )* (a r );

(a/b) X = a X /b X ;

(a X ) r = a (x*y) .

Tieto rovnosti budú platné pre všetky skutočné hodnoty x a y.

5. Graf exponenciálnej funkcie vždy prechádza bodom so súradnicami (0;1)

6. V závislosti od toho, či exponenciálna funkcia rastie alebo klesá, jej graf bude mať jeden z dvoch typov.

Nasledujúci obrázok ukazuje graf rastúcej exponenciálnej funkcie: a>0.

Nasledujúci obrázok je grafom klesajúcej exponenciálnej funkcie: 0

Bodom (0; 1) prechádza graf rastúcej exponenciálnej funkcie aj graf klesajúcej exponenciálnej funkcie podľa vlastnosti opísanej v piatom odseku.

7. Exponenciálna funkcia nemá extrémne body, to znamená, že nemá minimálne a maximálne body funkcie. Ak vezmeme do úvahy funkciu na akomkoľvek konkrétnom segmente, potom funkcia nadobudne minimálne a maximálne hodnoty na konci tohto intervalu.

8. Funkcia nie je párna ani nepárna. Exponenciálna funkcia je všeobecná funkcia. Vidno to aj z grafov, žiadny z nich nie je symetrický ani okolo osi Oy, ani okolo pôvodu.

Logaritmus

Logaritmy boli vždy brané do úvahy ťažká téma v školskej matematike. Existuje mnoho rôznych definícií logaritmu, ale z nejakého dôvodu väčšina učebníc používa tie najzložitejšie a najnešťastnejšie z nich.

Logaritmus definujeme jednoducho a jasne. Na to vytvoríme tabuľku:

Takže máme mocniny dvoch. Ak vezmete číslo zo spodného riadku, potom môžete ľahko nájsť silu, na ktorú musíte zdvihnúť dvojku, aby ste získali toto číslo. Napríklad, ak chcete získať 16, musíte zvýšiť dve na štvrtú mocninu. A aby ste získali 64, musíte zvýšiť dve na šiestu mocninu. To je možné vidieť z tabuľky.

A teraz - v skutočnosti definícia logaritmu:

Definícia

Logaritmus základ a z argumentu x je moc, na ktorú treba číslo zvýšiť a získať číslo X.

Označenie

log a x = b
kde a je základ, x je argument, b Čo presne je logaritmus.

Napríklad 2 3 = 8 ⇒ log 2 8 = 3 (základný 2 logaritmus čísla 8 je tri, pretože 2 3 = 8). Môže tiež log 2 64 = 6, pretože 2 6 = 64.

Zavolá sa operácia hľadania logaritmu čísla k danému základulogaritmus . Pridajme teda do tabuľky nový riadok:

Bohužiaľ, nie všetky logaritmy sa dajú ľahko zvážiť. Skúste napríklad nájsť log 2 5. Číslo 5 nie je v tabuľke, ale logika diktuje, že logaritmus bude ležať niekde na segmente. Pretože 22< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.

Takéto čísla sa nazývajú iracionálne: čísla za desatinnou čiarkou možno písať donekonečna a nikdy sa neopakujú. Ak sa logaritmus ukáže ako iracionálny, je lepšie ho nechať takto: log 2 5, log 3 8, log 5 100.

Je dôležité pochopiť, že logaritmus je výraz s dvoma premennými (základ a argument). Mnoho ľudí si spočiatku mýli, kde je základ a kde je argument. Aby ste predišli nepríjemným nedorozumeniam, stačí sa pozrieť na obrázok:

Pred nami nie je nič viac ako definícia logaritmu. Pamätajte: logaritmus je sila , ku ktorému je potrebné zvýšiť základ, aby ste dostali argument. Práve základ je mocne vyvýšený - na obrázku je zvýraznený červenou farbou. Ukazuje sa, že základňa je vždy na dne! Toto úžasné pravidlo hovorím svojim študentom na prvej hodine - a nie je tam žiadny zmätok.

Prišli sme na definíciu - zostáva sa naučiť počítať logaritmy, t.j. zbavte sa znaku „log“. Na začiatok poznamenávame Z definície vyplývajú dve dôležité skutočnosti:

Argument a základ musia byť vždy väčšie ako nula. Vyplýva to z definície stupňa racionálnym exponentom, na ktorý je zredukovaná definícia logaritmu.

Základ sa musí líšiť od jednoty, pretože jednotka k akejkoľvek moci je stále jednotkou. Z tohto dôvodu je otázka „na akú silu treba pozdvihnúť, aby sme dostali dve“ nezmyselná. Taký stupeň neexistuje!

Takéto obmedzenia volal platný rozsah(ODZ). Ukazuje sa, že ODZ logaritmu vyzerá takto: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Všimni si bez obmedzenia počtu b (hodnota logaritmu) sa neprekrýva. Napríklad logaritmus môže byť záporný: log 2 0,5 = −1, pretože 0,5 = 2 -1.

Teraz však uvažujeme iba o číselných výrazoch, kde nie je potrebné poznať ODZ logaritmu. Všetky obmedzenia už spracovatelia problémov vzali do úvahy. Keď však do hry vstúpia logaritmické rovnice a nerovnosti, požiadavky DHS sa stanú povinnými. Skutočne, v základe a argumente môžu byť veľmi silné konštrukcie, ktoré nemusia nevyhnutne zodpovedať vyššie uvedeným obmedzeniam.

Teraz zvážiť generála schéma na výpočet logaritmov. Pozostáva z troch krokov:

Odoslať nadáciu a a argument x vo forme titulu s minimom možný základ, veľké jednotky. Po ceste je lepšie zbaviť sa desatinných zlomkov;

Rozhodnite sa pre premennú b rovnica: x = a b ;

Prijaté číslo b bude odpoveďou.

To je všetko! Ak sa logaritmus ukáže ako iracionálny, bude to vidieť už v prvom kroku. Požiadavka, aby bol základ väčší ako jedna, je veľmi dôležitá: znižuje sa tým pravdepodobnosť chyby a výrazne sa zjednodušujú výpočty. Podobný desatinné miesta: ak ich hneď preložíte do obyčajných, chýb bude mnohonásobne menej.

Pozrime sa, ako táto schéma funguje konkrétne príklady:

Vypočítajte logaritmus: log 5 25

Predstavme si základ a argument ako mocninu päťky: 5 = 5 1 ; 25 = 52;

Zostavme a vyriešme rovnicu:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;

Dostal odpoveď: 2.

Vypočítajte logaritmus:

Predstavme si základ a argument ako mocninu troch: 3 = 3 1 ; 1/81 \u003d 81 -1 \u003d (3 4) -1 \u003d 3 -4;

Zostavme a vyriešme rovnicu:

Dostal som odpoveď: -4.

−4

Vypočítajte logaritmus: log 4 64

Predstavme si základ a argument ako mocninu dvoch: 4 = 2 2 ; 64 = 26;

Zostavme a vyriešme rovnicu:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3;

Dostal odpoveď: 3.

Vypočítajte logaritmus: log 16 1

Predstavme si základ a argument ako mocninu dvoch: 16 = 2 4 ; 1 = 20;

Zostavme a vyriešme rovnicu:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0;

Prijatá odpoveď: 0.

Vypočítajte logaritmus: log 7 14

Predstavme si základ a argument ako mocninu siedmich: 7 = 7 1 ; 14 nie je vyjadrené ako mocnina siedmich, pretože 7 1< 14 < 7 2 ;

Z predchádzajúceho odseku vyplýva, že logaritmus sa neuvažuje;

Odpoveď je žiadna zmena: log 7 14.

denník 7 14

Malá poznámka k poslednému príkladu. Ako sa uistiť, že číslo nie je presnou mocninou iného čísla? Veľmi jednoduché – stačí to rozložiť na prvočiniteľa. Ak sú v expanzii aspoň dva odlišné faktory, číslo nie je presnou mocninou.

Zistite, či sú presné mocniny čísla: 8; 48; 81; 35; štrnásť.

8 \u003d 2 2 2 \u003d 2 3 - presný stupeň, pretože existuje len jeden multiplikátor;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 nie je presná mocnina, pretože existujú dva faktory: 3 a 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - presný stupeň;
35 = 7 5 - opäť nie presný stupeň;
14 \u003d 7 2 - opäť nie presný stupeň;

8, 81 - presný stupeň; 48, 35, 14 - č.

Všimnite si tiež, že samotné prvočísla sú vždy presné mocniny samých seba.

Desatinný logaritmus

Niektoré logaritmy sú také bežné, že majú špeciálny názov a označenie.

Definícia

Desatinný logaritmus z argumentu x je logaritmus k základu 10, t.j. moc, na ktorú musíte zvýšiť číslo 10, aby ste získali číslo X.

Označenie

lg x

Napríklad log 10 = 1; log 100 = 2; lg 1000 = 3 - atď.

Keď sa odteraz v učebnici objaví fráza ako „Nájsť lg 0,01“, vedzte, že to nie je preklep. Toto je desiatkový logaritmus. Ak však na takéto označenie nie ste zvyknutí, vždy ho môžete prepísať:
log x = log 10 x

Všetko, čo platí pre bežné logaritmy, platí aj pre desatinné miesta.

prirodzený logaritmus

Existuje ďalší logaritmus, ktorý má svoj vlastný zápis. V istom zmysle je ešte dôležitejšia ako desatinná. Je to o o prirodzenom logaritme.

Definícia

prirodzený logaritmus z argumentu x je základný logaritmus e , t.j. moc, na ktorú treba číslo zvýšiť e získať číslo X.

Označenie

ln x

Mnohí sa budú pýtať: aké je číslo e? Ide o iracionálne číslo, jeho presná hodnota sa nedá nájsť a zapísať. Tu sú len prvé čísla:
e = 2,718281828459...

Nebudeme sa ponoriť do toho, čo je toto číslo a prečo je to potrebné. Len si pamätajte, že e je základom prirodzeného logaritmu:
ln x = log e x

Teda ln e = 1; loge2 = 2; V e 16 = 16 - atď. Na druhej strane, ln 2 je iracionálne číslo. Vo všeobecnosti je prirodzený logaritmus akéhokoľvek racionálneho čísla iracionálny. Samozrejme okrem jednoty: ln 1 = 0.

Pre prirodzené logaritmy platia všetky pravidlá, ktoré platia pre bežné logaritmy.

Základné vlastnosti logaritmov

Logaritmy, ako každé číslo, možno sčítať, odčítať a previesť všetkými možnými spôsobmi. Ale keďže logaritmy nie sú celkom bežné čísla, existujú pravidlá, ktoré sa nazývajú základné vlastnosti.

Tieto pravidlá musia byť známe - bez nich nemožno vyriešiť žiadny vážny logaritmický problém. Navyše je ich veľmi málo – všetko sa dá naučiť za jeden deň. Tak poďme na to.

Sčítanie a odčítanie logaritmov

Zvážte dva logaritmy s rovnakým základom: log a x a log a y . Potom ich možno sčítať a odčítať a:

log a x + denník a y = log a ( X · r );

log a x −log a y = log a ( X : r ).

takze súčet logaritmov sa rovná logaritmu súčinu a rozdiel je logaritmus kvocientu. Upozorňujeme: kľúčovým bodom sú rovnaké základy. Ak sú základy odlišné, tieto pravidlá nefungujú!

Tieto vzorce pomôžu vypočítať logaritmický výraz, aj keď sa neberú do úvahy jeho jednotlivé časti (pozri lekciu " "). Pozrite sa na príklady - a uvidíte:

Nájdite hodnotu výrazu: log 6 4 + log 6 9.

Keďže základy logaritmov sú rovnaké, použijeme súčtový vzorec:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

Nájdite hodnotu výrazu: log 2 48 − log 2 3.

Základy sú rovnaké, používame rozdielový vzorec:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

Nájdite hodnotu výrazu: log 3 135 − log 3 5.

Opäť platí, že základy sú rovnaké, takže máme:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

Ako vidíte, pôvodné výrazy sa skladajú zo „zlých“ logaritmov, ktoré sa neuvažujú samostatne. Ale po transformáciách sa ukážu celkom normálne čísla. Na základe tejto skutočnosti mnohí testovacie papiere. Áno, tá kontrola – podobné výrazy so všetkou vážnosťou (niekedy – prakticky bez zmien) sa ponúkajú na skúške.

Odstránenie exponentu z logaritmu

Teraz si úlohu trochu skomplikujeme. Čo ak existuje stupeň v základe alebo argumente logaritmu? Potom exponent tohto stupňa možno odobrať zo znamienka logaritmu podľa nasledujúcich pravidiel:

Je ľahké to vidieť posledné pravidlo nasleduje po prvých dvoch. Ale je lepšie si to aj tak zapamätať – v niektorých prípadoch to výrazne zníži množstvo výpočtov.

Samozrejme všetky tieto pravidlá dávajú zmysel, ak je dodržaný logaritmus ODZ: a > 0, a ≠ 1, x > 0 môžete zadať čísla pred znamienkom logaritmu do samotného logaritmu. To je to, čo sa najčastejšie vyžaduje.

Nájdite hodnotu výrazu: log 7 49 6 .

Zbavme sa stupňa v argumente podľa prvého vzorca:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

Nájdite hodnotu výrazu:

Všimnite si, že menovateľ je logaritmus, ktorého základ a argument sú presné mocniny: 16 = 2 4 ; 49 = 72. Máme:

Myslím, že posledný príklad potrebuje objasnenie. Kam zmizli logaritmy? Do poslednej chvíle pracujeme len s menovateľom. Uviedli základ a argument stojaceho logaritmu vo forme stupňov a vybrali ukazovatele - dostali „trojposchodový“ zlomok.

Teraz sa pozrime na hlavný zlomok. Čitateľ a menovateľ majú rovnaké číslo: log 2 7. Keďže log 2 7 ≠ 0, zlomok môžeme zmenšiť - 2/4 zostanú v menovateli. Podľa pravidiel aritmetiky môžu byť štyri prenesené do čitateľa, čo sa stalo. Výsledkom je odpoveď: 2.

Prechod na nový základ

Keď už hovoríme o pravidlách sčítania a odčítania logaritmov, osobitne som zdôraznil, že fungujú iba s rovnakými základmi. Čo ak sú základy odlišné? Čo ak to nie sú presné mocniny rovnakého čísla?

Na pomoc prichádzajú vzorce pre prechod na novú základňu. Formulujeme ich vo forme vety:

Veta

Nechajte logaritmus logovať a x . Potom pre ľubovoľné číslo c tak, že c > 0 a c ≠ 1, platí rovnosť:

Najmä ak dáme c = x, dostaneme:

Z druhého vzorca vyplýva, že je možné zameniť základ a argument logaritmu, ale v tomto prípade je celý výraz „prevrátený“, t.j. logaritmus je v menovateli.

Tieto vzorce sa zriedka nachádzajú v bežných číselných výrazoch. Ich vhodnosť je možné vyhodnotiť len pri riešení logaritmických rovníc a nerovníc.

Sú však úlohy, ktoré sa nedajú vyriešiť vôbec inak ako presťahovaním sa do nového základu. Uvažujme o niekoľkých z nich:

Nájdite hodnotu výrazu: log 5 16 log 2 25.

Všimnite si, že argumenty oboch logaritmov sú presné exponenty. Vyberme ukazovatele: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;

Teraz otočme druhý logaritmus:

Keďže súčin sa nemení permutáciou faktorov, pokojne sme vynásobili štyri a dva a potom sme vypočítali logaritmy.

Nájdite hodnotu výrazu: log 9 100 lg 3.

Základom a argumentom prvého logaritmu sú presné mocniny. Poďme si to zapísať a zbaviť sa indikátorov:

Teraz sa zbavme desiatkového logaritmu prechodom na nový základ:

Základná logaritmická identita

V procese riešenia je často potrebné reprezentovať číslo ako logaritmus k danej báze. V tomto prípade nám pomôžu vzorce:

V prvom prípade číslo n sa stáva exponentom argumentu. číslo n môže byť úplne čokoľvek, pretože je to len hodnota logaritmu.

Druhý vzorec je vlastne parafrázovaná definícia. Volá sa to takto:základná logaritmická identita.

Čo sa stane, ak sa číslo b zvýši do takej miery, že číslo b v tomto stupni dáva číslo a? Správne: toto je rovnaké číslo a. Ešte raz si pozorne prečítajte tento odsek – veľa ľudí na ňom „visí“.

Rovnako ako nové základné konverzné vzorce, základná logaritmická identita je niekedy jediným možným riešením.

Úloha

Nájdite hodnotu výrazu:

rozhodnutie

Všimnite si, že log 25 64 = log 5 8 - práve vytiahol štvorec zo základne a argument logaritmu. Vzhľadom na pravidlá násobenia právomocí s rovnakým základom dostaneme:

200

Ak niekto nevie, toto bola skutočná úloha zo skúšky :)

Logaritmická jednotka a logaritmická nula

Na záver uvediem dve identity, ktoré je ťažké nazvať vlastnosťami – skôr ide o dôsledky z definície logaritmu. Neustále sa nachádzajú v problémoch a prekvapivo robia problémy aj „pokročilým“ žiakom.

log a a = 1 je logaritmická jednotka. Pamätajte si raz a navždy: logaritmus na akúkoľvek základňu a z tejto základne sa rovná jednej.

log a 1 = 0 je logaritmická nula. Základňa a môže byť čokoľvek, ale ak je argument jedna - logaritmus je nula! pretože 0 = 1 je priamym dôsledkom definície.

To sú všetky vlastnosti. Určite si ich nacvičte v praxi!

lekcia č.2

Téma: Exponenciálna funkcia, jej vlastnosti a graf.

Cieľ: Skontrolujte kvalitu asimilácie konceptu „exponenciálnej funkcie“; rozvíjať zručnosti v rozpoznávaní exponenciálnej funkcie, v používaní jej vlastností a grafov, naučiť študentov používať analytické a grafické formy zaznamenávania exponenciálnej funkcie; poskytnúť pracovné prostredie v triede.

Vybavenie: tabule, plagáty

Formulár lekcie: učebňa

Typ lekcie: praktická lekcia

Typ lekcie: lekcia nácviku zručností

Plán lekcie

1. Organizačný moment

2. Samostatná práca a overovanie domáca úloha

3. Riešenie problémov

4. Zhrnutie

5. Domáce úlohy

Počas vyučovania.

1. Organizačný moment :

Ahoj. Otvorte zošity, zapíšte si dnešný dátum a tému hodiny „Exponenciálna funkcia“. Dnes budeme pokračovať v štúdiu exponenciálnej funkcie, jej vlastností a grafu.

2. Samostatná práca a kontrola domácich úloh .

Cieľ: skontrolovať kvalitu asimilácie pojmu „exponenciálna funkcia“ a skontrolovať splnenie teoretickej časti domácej úlohy

metóda: testovacia úloha, frontálny prieskum

Ako domácu úlohu ste dostali čísla z učebnice úloh a odsek z učebnice. Vykonávanie čísel z učebnice teraz nebudeme kontrolovať, ale zošity odovzdáte na konci hodiny. Teraz bude teória testovaná formou malého testu. Úloha je pre všetkých rovnaká: dostanete zoznam funkcií, musíte zistiť, ktoré z nich sú orientačné (podčiarknite ich). A k exponenciálnej funkcii treba napísať, či je rastúca alebo klesajúca.

možnosť 1 Odpoveď b) D) - exponenciálny, klesajúci	Možnosť 2 Odpoveď D) - exponenciálny, klesajúci D) - orientačný, zvyšujúci sa
Možnosť 3 Odpoveď ALE) - orientačný, zvyšujúci sa b) - exponenciálny, klesajúci	Možnosť 4 Odpoveď ALE) - exponenciálny, klesajúci AT) - orientačný, zvyšujúci sa

Teraz si spoločne pripomeňme, aká funkcia sa nazýva exponenciálna?

Funkcia tvaru , kde a , sa nazýva exponenciálna funkcia.

Aký je rozsah tejto funkcie?

Všetky reálne čísla.

Aký je rozsah exponenciálnej funkcie?

Všetky kladné reálne čísla.

Znižuje sa, ak je základ väčší ako nula, ale menší ako jedna.

Kedy klesá exponenciálna funkcia na svojom doméne?

Zvyšuje sa, ak je základňa väčšia ako jedna.

3. Riešenie problémov

Cieľ: rozvíjať zručnosti v rozpoznávaní exponenciálnej funkcie, v používaní jej vlastností a grafov, naučiť študentov používať analytické a grafické formy zaznamenávania exponenciálnej funkcie

Metóda: ukážka riešenia typických úloh učiteľom, ústna práca, práca pri tabuli, práca v zošite, rozhovor učiteľa so žiakmi.

Vlastnosti exponenciálnej funkcie možno využiť pri porovnávaní 2 a viacerých čísel. Napríklad: č. 000. Porovnajte hodnoty a ak a) ..gif" width="37" height="20 src=">, potom je to dosť zložitá úloha: museli by sme vziať odmocninu z 3 a 9 a porovnať ich. Vieme však, že sa to zvyšuje. je vo vlastnom rade znamená, že keď sa argument zvýši, hodnota funkcie sa zvýši, to znamená, že nám stačí porovnať hodnoty argumentu medzi sebou a samozrejme, že (možno demonštrovať na plagáte so zvyšujúcou sa exponenciálnou funkciou). A vždy pri riešení takýchto príkladov najskôr určte základ exponenciálnej funkcie, porovnajte s 1, určte monotónnosť a pristúpte k porovnávaniu argumentov. V prípade klesajúcej funkcie: ako argument rastie, hodnota funkcie klesá, preto sa pri prechode z nerovnosti argumentov na nerovnosť funkcií zmení znamienko nerovnosti. Potom riešime ústne: b)

-

AT)

-

G)

-

- č. 000. Porovnajte čísla: a) a

Preto sa funkcia zvyšuje

prečo?

Zvýšenie funkcie a

Preto funkcia klesá

Obe funkcie sa zvyšujú v celej svojej doméne definície, pretože sú exponenciálne so základom väčším ako jedna.

aký to má zmysel?

Vytvárame grafy:

Ktorá funkcia rastie rýchlejšie pri snahe https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">

Ktorá funkcia klesá rýchlejšie, keď sa snažíte https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">

Ktorá z funkcií má na intervale najväčšiu hodnotu v určitom bode?

D), https://pandia.ru/text/80/379/images/image068_0.gif" width="69" height="57 src=">. Najprv zistime rozsah týchto funkcií. zhodovať sa?

Áno, doménou týchto funkcií sú všetky reálne čísla.

Pomenujte rozsah každej z týchto funkcií.

Rozsahy týchto funkcií sa zhodujú: všetky kladné reálne čísla.

Určte typ monotónnosti každej z funkcií.

Všetky tri funkcie klesajú v celej svojej doméne definície, pretože sú exponenciálne so základom menším ako jedna a väčším ako nula.

Aký je singulárny bod grafu exponenciálnej funkcie?

aký to má zmysel?

Bez ohľadu na základ stupňa exponenciálnej funkcie, ak je exponent 0, potom je hodnota tejto funkcie 1.

Vytvárame grafy:

Poďme analyzovať grafy. Koľko priesečníkov majú grafy funkcií?

Ktorá funkcia sa pri úsilí znižuje rýchlejšie? https://pandia.ru/text/80/379/images/image070.gif

Ktorá funkcia rastie rýchlejšie, keď sa snažíte? https://pandia.ru/text/80/379/images/image070.gif

Ktorá z funkcií má na intervale najväčšiu hodnotu v určitom bode?

Ktorá z funkcií má na intervale najväčšiu hodnotu v určitom bode?

Prečo majú exponenciálne funkcie s rôznymi základňami iba jeden priesečník?

Exponenciálne funkcie sú prísne monotónne v celej svojej doméne definície, takže sa môžu pretínať iba v jednom bode.

Ďalšia úloha sa zameria na využitie tejto vlastnosti. № 000. Nájdite najväčšiu a najmenšiu hodnotu danej funkcie na danom intervale a). Pripomeňme, že striktne monotónna funkcia má svoje minimálne a maximálne hodnoty na konci daného intervalu. A ak sa funkcia zvyšuje, potom jej najvyššia hodnota bude na pravom konci segmentu a najmenší na ľavom konci segmentu (ukážka na plagáte s použitím exponenciálnej funkcie ako príkladu). Ak je funkcia klesajúca, jej najväčšia hodnota bude na ľavom konci segmentu a najmenšia na pravom konci segmentu (demonštrácia na plagáte s použitím exponenciálnej funkcie ako príkladu). Funkcia sa zvyšuje, pretože preto najmenšia hodnota funkcie bude v bode https://pandia.ru/text/80/379/images/image075_0.gif" width="145" height="29" >. Body b) , v) d) riešte zošity svojpomocne, skontrolujeme ústne.

Žiaci riešia úlohu vo svojom zošite

Funkcia klesania

Funkcia klesania najväčšia hodnota funkcie na intervale najmenšia hodnota funkcie na intervale

Zvyšujúca sa funkcia najmenšia hodnota funkcie na intervale najväčšia hodnota funkcie na intervale

- № 000. Nájdite najväčšiu a najmenšiu hodnotu danej funkcie na danom intervale a) . Táto úloha je takmer rovnaká ako predchádzajúca. Ale tu nie je daný segment, ale lúč. Vieme, že funkcia sa zvyšuje a nemá ani najväčšiu, ani najmenšiu hodnotu na celom číselnom rade https://pandia.ru/text/80/379/images/image063_0.gif" width="68" height = "20"> a má tendenciu k , t.j. na lúči má funkcia at tendenciu k 0, ale nemá vlastnú najmenšia hodnota, ale v bode má najväčšiu hodnotu . Body b) , v) , G) Vyriešte si vlastné zošity, skontrolujeme to ústne.

Najprv predstavíme definíciu exponenciálnej funkcie.

Exponenciálna funkcia $f\left(x\right)=a^x$, kde $a >1$.

Predstavme si vlastnosti exponenciálnej funkcie pre $a >1$.

\ \[bez koreňov\] \

Priesečník so súradnicovými osami. Funkcia nepretína os $Ox$, ale pretína os $Oy$ v bode $(0,1)$.

$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$

\ \[bez koreňov\] \

Graf (obr. 1).

Obrázok 1. Graf funkcie $f\left(x\right)=a^x,\ pre \ a >1$.

Exponenciálna funkcia $f\left(x\right)=a^x$, kde $0

Predstavme si vlastnosti exponenciálnej funkcie pre $0

Oblasťou definície sú všetky reálne čísla.

$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- funkcia nie je ani párna, ani nepárna.

$f(x)$ je spojité na celej doméne definície.

Rozsah hodnôt je interval $(0,+\infty)$.

$f"(x)=\vľavo(a^x\vpravo)"=a^xlna$

\ \[bez koreňov\] \ \[bez koreňov\] \

Funkcia je konvexná v celej oblasti definície.

Správanie na konci rozsahu:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]

Graf (obr. 2).

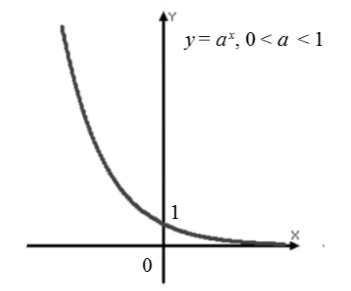
Príklad úlohy na zostrojenie exponenciálnej funkcie

Preskúmajte a nakreslite funkciu $y=2^x+3$.

rozhodnutie.

Urobme štúdiu na príklade vyššie uvedenej schémy:

Oblasťou definície sú všetky reálne čísla.

$f\left(-x\right)=2^(-x)+3$ -- funkcia nie je ani párna, ani nepárna.

$f(x)$ je spojité na celej doméne definície.

Rozsah hodnôt je interval $(3,+\infty)$.

$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$

Funkcia sa zvyšuje v celej oblasti definície.

$f(x)\ge 0$ cez celú doménu definície.

Priesečník so súradnicovými osami. Funkcia nepretína os $Ox$, ale pretína os $Oy$ v bode ($0,4)$

$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$

Funkcia je konvexná v celej oblasti definície.

Správanie na konci rozsahu:

\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]

Graf (obr. 3).

Obrázok 3. Graf funkcie $f\left(x\right)=2^x+3$