Koncentracja uwagi:
Definicja. Funkcjonować nazywa się gatunek funkcja wykładnicza .
Komentarz. Wykluczenie podstawowe A cyfry 0; 1 i wartości ujemne A wyjaśnić następującymi okolicznościami:
Samo wyrażenie analityczne x w takich przypadkach zachowuje swoje znaczenie i można go napotkać przy rozwiązywaniu problemów. Na przykład dla wyrażenia x y kropka x = 1; y = 1 wchodzi w zakres dopuszczalnych wartości.
Skonstruować wykresy funkcji: i .
 |
 |
| Wykres funkcji wykładniczej | |
| y= A X, a > 1 | y= A X , 0< a < 1 |
 |
 |
Własności funkcji wykładniczej
| Własności funkcji wykładniczej | y= A X, a > 1 | y= A X , 0< a < 1 |
|
||
| 2. Zakres wartości funkcji | ||
| 3. Przedziały porównania z jednostką | Na X> 0, za X > 1 | Na X > 0, 0< a X < 1 |
| Na X < 0, 0< a X < 1 | Na X < 0, a X > 1 | |
| 4. Parzyste, nieparzyste. | Funkcja nie jest ani parzysta, ani nieparzysta (funkcja ogólna). | |
| 5. Monotonia. | wzrasta monotonicznie o R | maleje monotonicznie o R |
| 6. Skrajności. | Funkcja wykładnicza nie ma skrajności. | |
| 7.Asymptota | Oś O X jest asymptotą poziomą. | |
| 8. Dla dowolnych wartości rzeczywistych X I y; |  |
|
Gdy stół jest wypełniony, zadania są rozwiązywane równolegle z wypełnieniem.
Zadanie numer 1. (Aby znaleźć dziedzinę funkcji).
Jakie wartości argumentów są ważne dla funkcji:
Zadanie nr 2. (Aby znaleźć zakres funkcji).
Rysunek przedstawia wykres funkcji. Określ zakres i zasięg funkcji:
 |
 |
 |
 |
Zadanie nr 3. (Aby wskazać przedziały porównania z jednostką).
Porównaj każdą z poniższych mocy z jedną:
Zadanie nr 4. (Aby zbadać funkcję pod kątem monotoniczności).
Porównaj liczby rzeczywiste według wielkości M I N Jeśli:
Zadanie nr 5. (Aby zbadać funkcję pod kątem monotoniczności).
Wyciągnij wniosek na temat podstawy A, Jeśli:
y(x) = 10 x ; f(x) = 6 x ; z(x) - 4x
Jak wykresy funkcji wykładniczych odnoszą się do siebie dla x > 0, x = 0, x< 0?
W jednej płaszczyźnie współrzędnych kreślone są wykresy funkcji:
y(x) = (0,1) x ; f(x) = (0,5) x ; z(x) = (0,8) x .
Jak wykresy funkcji wykładniczych odnoszą się do siebie dla x > 0, x = 0, x< 0?
| Numer
jedną z najważniejszych stałych w matematyce. Z definicji to równa granicy ciągu
z nieograniczoną
rosnący n
. Przeznaczenie mi wprowadzony Leonarda Eulera
w 1736 r. Obliczył pierwsze 23 cyfry tej liczby w zapisie dziesiętnym, a samą liczbę nazwano na cześć Napiera „liczbą nierównorzędną”.
Numer mi odgrywa szczególną rolę w analizie matematycznej. Funkcja wykładnicza z podstawą mi, zwany wykładnikiem i oznaczone y = mi x. Pierwsze znaki liczby miłatwe do zapamiętania: dwa, przecinek, siedem, rok urodzenia Lwa Tołstoja - dwa razy, czterdzieści pięć, dziewięćdziesiąt, czterdzieści pięć. |
 |
Praca domowa:
Kołmogorow s. 35; nr 445-447; 451; 453.
Powtórz algorytm konstruowania wykresów funkcji zawierających zmienną pod znakiem modułu.
Funkcja wykładnicza
Funkcja postaci y = a X , gdzie a jest większe od zera, a a nie jest równe jeden, nazywamy funkcją wykładniczą. Główne właściwości funkcji wykładniczej:
1. Dziedziną funkcji wykładniczej będzie zbiór liczb rzeczywistych.
2. Zakres funkcji wykładniczej będzie zbiorem wszystkich dodatnich liczb rzeczywistych. Czasami ten zestaw jest oznaczany jako R+ dla zwięzłości.
3. Jeżeli w funkcji wykładniczej podstawa a jest większa niż jeden, to funkcja będzie rosnąca w całej dziedzinie definicji. Jeśli funkcja wykładnicza dla podstawy a spełnia następujący warunek 0
4. Obowiązują wszystkie podstawowe właściwości stopni. Główne właściwości stopni są reprezentowane przez następujące równości:
A X *A y = za (x+y) ;
(A X )/(A y ) = za (xy) ;
(a*b) X = (a X )*(A y );
(a/b) X = za X /B X ;
(A X ) y = za (x*y) .
Te równości będą obowiązywać dla wszystkich rzeczywistych wartości x i y.
5. Wykres funkcji wykładniczej zawsze przechodzi przez punkt o współrzędnych (0;1)
6. W zależności od tego, czy funkcja wykładnicza rośnie, czy maleje, jej wykres będzie miał jeden z dwóch typów.
Poniższy rysunek przedstawia wykres rosnącej funkcji wykładniczej: a>0.
Poniższy rysunek jest wykresem malejącej funkcji wykładniczej: 0
Zarówno wykres rosnącej funkcji wykładniczej, jak i wykres malejącej funkcji wykładniczej, zgodnie z właściwością opisaną w akapicie piątym, przechodzą przez punkt (0; 1).
7. Funkcja wykładnicza nie ma punktów ekstremalnych, czyli innymi słowy nie ma punktów minimalnych i maksymalnych funkcji. Jeśli weźmiemy pod uwagę funkcję na dowolnym segmencie, to funkcja przyjmie wartości minimalne i maksymalne na końcach tego przedziału.
8. Funkcja nie jest parzysta ani nieparzysta. Funkcja wykładnicza jest funkcją ogólną. Można to również zobaczyć na wykresach, żaden z nich nie jest symetryczny ani względem osi Oy, ani względem początku.
Logarytm
Logarytmy zawsze były brane pod uwagę trudny temat w matematyce szkolnej. Istnieje wiele różnych definicji logarytmu, ale z jakiegoś powodu większość podręczników używa najbardziej złożonej i niefortunnej z nich.
Logarytm zdefiniujemy prosto i jasno. Stwórzmy w tym celu tabelę:
Mamy więc potęgę dwójki. Jeśli weźmiesz liczbę z dolnej linii, możesz łatwo znaleźć potęgę, do której musisz podnieść dwójkę, aby uzyskać tę liczbę. Na przykład, aby uzyskać 16, musisz podnieść dwa do czwartej potęgi. Aby uzyskać 64, musisz podnieść dwa do szóstej potęgi. To widać z tabeli.
A teraz - właściwie definicja logarytmu:
Definicja
Logarytm oprzyj a na podstawie argumentu x jest potęgą, do której należy podnieść liczbę A aby uzyskać numer X.
Przeznaczenie
logarytm a x = b
gdzie a to podstawa, x to argument, b Czym dokładnie jest logarytm.
Na przykład 2 3 = 8 ⇒ log 2 8 = 3 (logarytm o podstawie 2 z 8 to trzy, ponieważ 2 3 = 8). Równie dobrze można zapisać 2 64 = 6, ponieważ 2 6 = 64.
Nazywa się operację znajdowania logarytmu liczby o podanej podstawielogarytm . Dodajmy więc nowy wiersz do naszej tabeli:
Niestety, nie wszystkie logarytmy są rozpatrywane tak łatwo. Na przykład spróbuj znaleźć log 2 5. Cyfry 5 nie ma w tabeli, ale logika podpowiada, że logarytm będzie leżeć gdzieś w segmencie. Ponieważ 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Takie liczby nazywane są niewymiernymi: liczby po przecinku można zapisywać w nieskończoność i nigdy się nie powtarzają. Jeśli logarytm okaże się niewymierny, lepiej zostawić go w ten sposób: log 2 5, log 3 8, log 5 100.
Ważne jest, aby zrozumieć, że logarytm jest wyrażeniem z dwiema zmiennymi (podstawą i argumentem). Na początku wiele osób myli, gdzie jest podstawa, a gdzie jest argument. Aby uniknąć irytujących nieporozumień, wystarczy spojrzeć na zdjęcie:
Przed nami nic więcej niż definicja logarytmu. Pamiętaj: logarytm jest potęgą , do którego musisz podnieść podstawę, aby uzyskać argument. Jest to podstawa podniesiona do potęgi - na obrazku zaznaczona na czerwono. Okazuje się, że podstawa jest zawsze na dole! Tę cudowną zasadę powtarzam moim uczniom już na pierwszej lekcji – i nie ma zamieszania.
Ustaliliśmy definicję - pozostaje nauczyć się liczyć logarytmy, tj. pozbyć się znaku „log”. Na początek zauważamy, że Z definicji wynikają dwa ważne fakty:
Argument i podstawa muszą być zawsze większe od zera. Wynika to z definicji stopnia wykładnikiem wymiernym, do którego sprowadza się definicja logarytmu.
Podstawa musi być różna od jedności, ponieważ jednostka do dowolnej potęgi jest nadal jednostką. Z tego powodu pytanie „do jakiej potęgi trzeba podnieść jednego, aby otrzymać dwa” jest bezsensowne. Nie ma takiego stopnia!
Takie ograniczenia zwany Prawidłowy zakres(ODZ). Okazuje się, że ODZ logarytmu wygląda tak: log za x = b ⇒ x > 0, a > 0, a ≠ 1.
Zauważ, że bez limitu liczby B (wartość logarytmu) nie nakłada się. Na przykład logarytm może być ujemny: log 2 0,5 = −1, ponieważ 0,5 = 2-1 .
Jednak teraz rozważamy tylko wyrażenia liczbowe, w których nie jest wymagana znajomość ODZ logarytmu. Wszystkie ograniczenia zostały już uwzględnione przez kompilatorów problemów. Ale kiedy w grę wchodzą równania i nierówności logarytmiczne, wymagania DHS staną się obowiązkowe. Rzeczywiście, w podstawie i argumentacji mogą znajdować się bardzo mocne konstrukcje, które niekoniecznie odpowiadają powyższym ograniczeniom.
Teraz rozważ generała schemat obliczania logarytmów. Składa się z trzech kroków:
Prześlij Fundację a i argument x w formie dyplomu z min możliwa podstawa, duże jednostki. Po drodze lepiej pozbyć się ułamków dziesiętnych;
Zdecyduj się na zmienną b równanie: x = a b ;
Otrzymany numer b będzie odpowiedzią.
To wszystko! Jeśli logarytm okaże się niewymierny, będzie to widoczne już na pierwszym etapie. Wymóg, aby podstawa była większa niż jeden, jest bardzo istotny: zmniejsza to prawdopodobieństwo błędu i znacznie upraszcza obliczenia. Podobny do dziesiętne: jeśli od razu przetłumaczysz je na zwykłe, błędów będzie wielokrotnie mniej.
Zobaczmy, jak działa ten schemat konkretne przykłady:
Oblicz logarytm: log 5 25
Przedstawmy podstawę i argument jako potęgę pięciu: 5 = 5 1 ; 25 = 52;
Zróbmy i rozwiążmy równanie:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
Otrzymał odpowiedź: 2.
Oblicz logarytm:
Przedstawmy podstawę i argument jako potęgę trzech: 3 = 3 1 ; 1/81 \u003d 81 -1 \u003d (3 4) -1 \u003d 3 -4;
Zróbmy i rozwiążmy równanie:
Otrzymałem odpowiedź: -4.
−4
Oblicz logarytm: log 4 64
Przedstawmy podstawę i argument jako potęgę dwójki: 4 = 2 2 ; 64 = 26;
Zróbmy i rozwiążmy równanie:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2 b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
Otrzymał odpowiedź: 3.
Oblicz logarytm: log 16 1
Przedstawmy podstawę i argument jako potęgę dwójki: 16 = 2 4 ; 1 = 20;
Zróbmy i rozwiążmy równanie:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4 b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
Otrzymano odpowiedź: 0.
Oblicz logarytm: log 7 14
Przedstawmy podstawę i argument jako potęgę siódemki: 7 = 7 1 ; 14 nie jest reprezentowane jako potęga siódemki, ponieważ 7 1< 14 < 7 2 ;
Z poprzedniego akapitu wynika, że logarytm nie jest brany pod uwagę;
Odpowiedź brzmi: bez zmian: log 7 14.
dziennik 7 14
Mała uwaga do ostatniego przykładu. Jak upewnić się, że liczba nie jest dokładną potęgą innej liczby? Bardzo proste - wystarczy rozłożyć to na czynniki pierwsze. Jeśli w rozszerzeniu występują co najmniej dwa różne czynniki, liczba nie jest dokładną potęgą.
Dowiedz się, czy dokładne potęgi liczby to: 8; 48; 81; 35; 14.
8 \u003d 2 2 2 \u003d 2 3 - dokładny stopień, ponieważ jest tylko jeden mnożnik;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 nie jest potęgą ścisłą, ponieważ są dwa czynniki: 3 i 2;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - dokładny stopień;
35 = 7 5 - znowu nie dokładny stopień;
14 \u003d 7 2 - znowu nie dokładny stopień;
8, 81 - dokładny stopień; 48, 35, 14 - nie.
Zauważ również, że same liczby pierwsze są zawsze dokładnymi potęgami samych siebie.
Logarytm dziesiętny
Niektóre logarytmy są tak powszechne, że mają specjalną nazwę i oznaczenie.
Definicja
Logarytm dziesiętny z argumentu x jest logarytmem o podstawie 10, tj. potęgę, do której należy podnieść liczbę 10, aby otrzymać tę liczbę X.
Przeznaczenie
lg x
Na przykład log 10 = 1; dziennik 100 = 2; lg 1000 = 3 - itd.
Od teraz, gdy w podręczniku pojawi się fraza „Znajdź lg 0.01”, wiedz, że to nie jest literówka. To jest logarytm dziesiętny. Jeśli jednak nie jesteś przyzwyczajony do takiego oznaczenia, zawsze możesz je przepisać:
log x = log 10 x
Wszystko, co jest prawdziwe dla logarytmów zwykłych, jest również prawdziwe dla ułamków dziesiętnych.
naturalny logarytm
Istnieje inny logarytm, który ma swój własny zapis. W pewnym sensie jest to nawet ważniejsze niż liczba dziesiętna. To jest o o logarytmie naturalnym.
Definicja
naturalny logarytm z argumentu x jest logarytmem bazowym mi , tj. potęgę, do której należy podnieść liczbę mi aby uzyskać numer X.
Przeznaczenie
ln x
Wielu zapyta: jaka jest liczba e? Jest to liczba niewymierna, jej dokładnej wartości nie można znaleźć i zapisać. Oto tylko pierwsze liczby:
e = 2,718281828459...
Nie będziemy zagłębiać się w to, czym jest ta liczba i dlaczego jest potrzebna. Tylko pamiętaj, e jest podstawą logarytmu naturalnego:
ln x = log mi x
Zatem ln e = 1; log e 2 = 2; w e 16 = 16 - itd. Z drugiej strony ln 2 jest liczbą niewymierną. Ogólnie rzecz biorąc, logarytm naturalny dowolnej liczby wymiernej jest niewymierny. Oprócz, oczywiście, jedności: ln 1 = 0.
W przypadku logarytmów naturalnych obowiązują wszystkie zasady, które są prawdziwe dla logarytmów zwykłych.
Podstawowe własności logarytmów
Logarytmy, jak każdą liczbę, można dodawać, odejmować i konwertować na wszelkie możliwe sposoby. Ale ponieważ logarytmy nie są całkiem zwykłymi liczbami, istnieją tutaj reguły, które nazywane są podstawowymi właściwościami.
Te zasady muszą być znane - bez nich nie da się rozwiązać żadnego poważnego problemu logarytmicznego. Ponadto jest ich bardzo mało - wszystkiego można się nauczyć w jeden dzień. Więc zacznijmy.
Dodawanie i odejmowanie logarytmów
Rozważ dwa logarytmy o tej samej podstawie: log a x i zaloguj a y . Następnie można je dodawać i odejmować oraz:
dziennik x + dziennik tak = dziennik A ( X · y );
dziennik x −log tak = dziennik A ( X : y ).
Więc, suma logarytmów jest równa logarytmowi iloczynu, a różnica jest logarytmem ilorazu. Uwaga: kluczową kwestią są tutaj te same bazy. Jeśli podstawy są różne, te zasady nie działają!
Te wzory pomogą ci obliczyć wyrażenie logarytmiczne, nawet jeśli nie uwzględniono jego poszczególnych części (patrz lekcja „ "). Spójrz na przykłady - i zobacz:
Znajdź wartość wyrażenia: log 6 4 + log 6 9.
Ponieważ podstawy logarytmów są takie same, używamy wzoru na sumę:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Znajdź wartość wyrażenia: log 2 48 − log 2 3.
Podstawy są takie same, używamy wzoru na różnicę:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Znajdź wartość wyrażenia: log 3 135 − log 3 5.
Ponownie, podstawy są takie same, więc mamy:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Jak widać, oryginalne wyrażenia składają się z „złych” logarytmów, które nie są rozpatrywane osobno. Ale po przekształceniach pojawiają się całkiem normalne liczby. Opierając się na tym fakcie, wielu papiery testowe. Tak, ta kontrola - podobne wyrażenia z całą powagą (czasami - praktycznie bez zmian) są oferowane na egzaminie.
Usuwanie wykładnika z logarytmu
Teraz skomplikujmy trochę zadanie. Co jeśli w podstawie lub argumencie logarytmu jest stopień? Następnie wykładnik tego stopnia można wyjąć ze znaku logarytmu zgodnie z następującymi zasadami:
Łatwo to zauważyć ostatnia zasada podąża za dwoma pierwszymi. Ale i tak lepiej o tym pamiętać - w niektórych przypadkach znacznie zmniejszy to ilość obliczeń.
Oczywiście wszystkie te zasady mają sens, jeśli obserwuje się logarytm ODZ: a > 0, a ≠ 1, x > 0 możesz wprowadzić liczby przed znakiem logarytmu do samego logarytmu. To jest najczęściej wymagane.
Znajdź wartość wyrażenia: log 7 49 6 .
Pozbądźmy się stopnia w argumencie według pierwszego wzoru:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Znajdź wartość wyrażenia:
Zauważ, że mianownik jest logarytmem, którego podstawą i argumentem są potęgi dokładne: 16 = 2 4 ; 49 = 72. Mamy:
Myślę, że ostatni przykład wymaga wyjaśnienia. Gdzie się podziały logarytmy? Do ostatniej chwili pracujemy tylko z mianownikiem. Przedstawili podstawę i argument stojącego tam logarytmu w postaci stopni i wyjęli wskaźniki - otrzymali ułamek „trzypiętrowy”.
Teraz spójrzmy na ułamek główny. Licznik i mianownik mają tę samą liczbę: log 2 7. Ponieważ log 2 7 ≠ 0, możemy skrócić ułamek - 2/4 pozostanie w mianowniku. Zgodnie z zasadami arytmetyki czwórkę można przenieść do licznika, co zostało zrobione. Wynikiem jest odpowiedź: 2.
Przejście na nowy fundament
Mówiąc o zasadach dodawania i odejmowania logarytmów, wyraźnie podkreśliłem, że działają one tylko z tymi samymi podstawami. A co jeśli podstawy są inne? Co jeśli nie są to dokładne potęgi tej samej liczby?
Na ratunek przychodzą formuły przejścia do nowej bazy. Formułujemy je w postaci twierdzenia:
Twierdzenie
Niech logarytm się zaloguje x . Następnie dla dowolnej liczby c takie, że c > 0 i c ≠ 1, równość jest prawdziwa:
W szczególności, jeśli umieścimy c = x, otrzymujemy:
Z drugiej formuły wynika, że można zamienić podstawę i argument logarytmu, ale w tym przypadku całe wyrażenie jest „odwrócone”, tj. logarytm jest w mianowniku.
Formuły te rzadko występują w zwykłych wyrażeniach liczbowych. Można ocenić, jak wygodne są tylko przy rozwiązywaniu logarytmicznych równań i nierówności.
Są jednak zadania, których w ogóle nie można rozwiązać, chyba że przeprowadzi się do nowego fundamentu. Rozważmy kilka z nich:
Znajdź wartość wyrażenia: log 5 16 log 2 25.
Zauważ, że argumenty obu logarytmów są dokładnymi wykładnikami. Wyjmijmy wskaźniki: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2 log 2 5;
Teraz odwróćmy drugi logarytm:
Ponieważ iloczyn nie zmienia się z permutacji czynników, spokojnie pomnożyliśmy cztery i dwa, a następnie obliczyliśmy logarytmy.
Znajdź wartość wyrażenia: log 9 100 lg 3.
Podstawą i argumentem pierwszego logarytmu są potęgi dokładne. Zapiszmy to i pozbądźmy się wskaźników:
Teraz pozbądźmy się logarytmu dziesiętnego, przechodząc do nowej podstawy:
Podstawowa tożsamość logarytmiczna
Często w procesie rozwiązywania wymagane jest przedstawienie liczby jako logarytmu do danej podstawy. W takim przypadku formuły pomogą nam:
W pierwszym przypadku liczba N staje się wykładnikiem argumentu. Numer N może być absolutnie wszystkim, ponieważ jest to po prostu wartość logarytmu.
Druga formuła jest w rzeczywistości sparafrazowaną definicją. Nazywa się to tak:podstawowa tożsamość logarytmiczna.
Rzeczywiście, co się stanie, jeśli liczba b zostanie podniesiona do takiego stopnia, że liczba b w tym stopniu da liczbę a? Zgadza się: to jest ta sama liczba a. Przeczytaj uważnie ten akapit jeszcze raz - wiele osób się na nim "wiesza".
Podobnie jak nowe formuły konwersji bazowej, podstawowa tożsamość logarytmiczna jest czasami jedynym możliwym rozwiązaniem.
Zadanie
Znajdź wartość wyrażenia:
Rozwiązanie
Zauważ, że log 25 64 = log 5 8 - właśnie wyjąłem kwadrat z podstawy i argument logarytmu. Biorąc pod uwagę zasady mnożenia potęg o tej samej podstawie, otrzymujemy:
200
Jeśli ktoś nie wie, to było prawdziwe zadanie z egzaminu :)
Jednostka logarytmiczna i zero logarytmiczne
Na zakończenie podam dwie tożsamości, które trudno nazwać własnościami – są to raczej konsekwencje z definicji logarytmu. Ciągle znajdują się w problemach i, co zaskakujące, stwarzają problemy nawet dla „zaawansowanych” uczniów.
log a a = 1 jest jednostka logarytmiczna. Zapamiętaj raz na zawsze: logarytm do dowolnej podstawy A z samej tej podstawy jest równy jeden.
log a 1 = 0 jest zero logarytmiczne. podstawa może być cokolwiek, ale jeśli argumentem jest jeden - logarytm wynosi zero! Ponieważ 0 = 1 jest bezpośrednią konsekwencją definicji.
To wszystkie właściwości. Pamiętaj, aby ćwiczyć wprowadzanie ich w życie!
Lekcja #2
Temat: Funkcja wykładnicza, jej własności i wykres.
Cel: Sprawdź jakość przyswojenia pojęcia „funkcji wykładniczej”; wyrobienie umiejętności rozpoznawania funkcji wykładniczej, posługiwania się jej własnościami i wykresami, nauczenie studentów posługiwania się analitycznymi i graficznymi formami zapisu funkcji wykładniczej; zapewnić warunki pracy w klasie.
Sprzęt: tablica, plakaty
Formularz lekcji: klasa
Rodzaj lekcji: lekcja praktyczna
Rodzaj lekcji: lekcja treningu umiejętności
Plan lekcji
1. Moment organizacyjny
2. Samodzielna praca i weryfikacja Praca domowa
3. Rozwiązywanie problemów
4. Podsumowanie
5. Praca domowa
Podczas zajęć.
1. Moment organizacyjny :
Cześć. Otwórz zeszyty, zapisz dzisiejszą datę i temat lekcji „Funkcja wykładnicza”. Dzisiaj będziemy kontynuować badanie funkcji wykładniczej, jej właściwości i wykresu.
2. Samodzielna praca i sprawdzanie prac domowych .
Cel: sprawdzić jakość przyswojenia pojęcia „funkcji wykładniczej” oraz sprawdzić wykonanie części teoretycznej pracy domowej
Metoda: zadanie testowe, badanie frontalne
Jako pracę domową otrzymaliście liczby z zeszytu zadań i akapit z podręcznika. Nie będziemy teraz sprawdzać wykonania numerów z podręcznika, ale zeszyty przekażesz na koniec lekcji. Teraz teoria zostanie sprawdzona w formie małego testu. Zadanie jest takie samo dla wszystkich: dostajesz listę funkcji, musisz dowiedzieć się, które z nich są orientacyjne (podkreśl je). A obok funkcji wykładniczej musisz napisać, czy rośnie, czy maleje.
opcja 1 Odpowiedź B) D) - wykładniczy, malejący | Opcja 2 Odpowiedź D) - wykładniczy, malejący D) - orientacyjny, rosnący |
Opcja 3 Odpowiedź A) - orientacyjny, rosnący B) - wykładniczy, malejący | Opcja 4 Odpowiedź A) - wykładniczy, malejący W) - orientacyjny, rosnący |
Przypomnijmy sobie teraz razem, jaka funkcja nazywa się wykładniczą?
Funkcja postaci , gdzie i , nazywana jest funkcją wykładniczą.
Jaki jest zakres tej funkcji?
Wszystkie liczby rzeczywiste.
Jaki jest zakres funkcji wykładniczej?
Wszystkie dodatnie liczby rzeczywiste.
Zmniejsza się, jeśli podstawa jest większa od zera, ale mniejsza od jeden.
Kiedy funkcja wykładnicza maleje w swojej dziedzinie?
Zwiększa się, jeśli podstawa jest większa niż jeden.
3. Rozwiązywanie problemów
Cel: kształtowanie umiejętności rozpoznawania funkcji wykładniczej, korzystania z jej własności i wykresów, nauczenie studentów korzystania z analitycznych i graficznych form zapisu funkcji wykładniczej
metoda: pokaz przez nauczyciela rozwiązywania typowych problemów, praca ustna, praca przy tablicy, praca w zeszycie, rozmowa nauczyciela z uczniami.
Właściwości funkcji wykładniczej można wykorzystać przy porównywaniu 2 lub więcej liczb. Na przykład: nr 000. Porównaj wartości i jeśli a) 
..gif" width="37" height="20 src=">, to jest to dość trudne zadanie: musielibyśmy wziąć pierwiastek sześcienny z 3 i 9 i porównać je. Ale wiemy, że zwiększa się, to jest we własnej kolejce oznacza, że wraz ze wzrostem argumentu rośnie wartość funkcji, czyli wystarczy, że porównamy ze sobą wartości argumentu i oczywiście, że 
(można zademonstrować na plakacie z rosnącą funkcją wykładniczą). I zawsze rozwiązując takie przykłady, najpierw określ podstawę funkcji wykładniczej, porównaj z 1, określ monotoniczność i przystąp do porównania argumentów. W przypadku funkcji malejącej: wraz ze wzrostem argumentu wartość funkcji maleje, dlatego przy przejściu od nierówności argumentów do nierówności funkcji zmienia się znak nierówności. Następnie rozwiązujemy ustnie: b) 
- 
W) 
- 
G) 
- 
- nr 000. Porównaj liczby: a) i
Zatem funkcja jest rosnąca
Dlaczego ?
Funkcja rosnąca i 
Zatem funkcja jest malejąca 
Obie funkcje rosną w całej swojej dziedzinie definicji, ponieważ są wykładnicze z podstawą większą niż jeden.
Jakie jest tego znaczenie?
Budujemy wykresy:
Która funkcja rośnie szybciej podczas dążenia https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">
Która funkcja zmniejsza się szybciej podczas dążenia https://pandia.ru/text/80/379/images/image062_0.gif" width="20 height=25" height="25">
Na przedziale, która z funkcji ma największą wartość w określonym punkcie?
D), https://pandia.ru/text/80/379/images/image068_0.gif" width="69" height="57 src=">. Najpierw dowiedzmy się, jaki jest zakres tych funkcji. zbiec się?
Tak, dziedziną tych funkcji są wszystkie liczby rzeczywiste.
Nazwij zakres każdej z tych funkcji.
Zakresy tych funkcji pokrywają się: wszystkie dodatnie liczby rzeczywiste.
Określ typ monotoniczności każdej z funkcji.
Wszystkie trzy funkcje maleją w całej swojej dziedzinie definicji, ponieważ są wykładnicze z podstawą mniejszą niż jeden i większą niż zero.
Jaki jest punkt osobliwy wykresu funkcji wykładniczej?
Jakie jest tego znaczenie?
Bez względu na podstawę stopnia funkcji wykładniczej, jeśli wykładnik wynosi 0, to wartość tej funkcji wynosi 1.
Budujemy wykresy:
Przeanalizujmy wykresy. Ile punktów przecięcia mają wykresy funkcji?
Która funkcja zmniejsza się szybciej podczas wysiłku? https://pandia.ru/text/80/379/images/image070.gif
Która funkcja rośnie szybciej podczas wysiłku? https://pandia.ru/text/80/379/images/image070.gif
Na przedziale, która z funkcji ma największą wartość w określonym punkcie?
Na przedziale, która z funkcji ma największą wartość w określonym punkcie?
Dlaczego funkcje wykładnicze o różnych podstawach mają tylko jeden punkt przecięcia?
Funkcje wykładnicze są ściśle monotoniczne w całej swojej dziedzinie definicji, więc mogą przecinać się tylko w jednym punkcie.
Następne zadanie skupi się na używaniu tej właściwości. № 000. Znajdź największą i najmniejszą wartość danej funkcji w danym przedziale a). Przypomnijmy, że funkcja ściśle monotoniczna przyjmuje swoje wartości minimalne i maksymalne na końcach danego przedziału. A jeśli funkcja jest rosnąca, to jej najwyższa wartość będzie na prawym końcu segmentu, a najmniejszy na lewym końcu segmentu (demonstracja na plakacie na przykładzie funkcji wykładniczej). Jeżeli funkcja jest malejąca, to jej największa wartość będzie na lewym końcu segmentu, a najmniejsza na prawym końcu segmentu (pokaz na plakacie na przykładzie funkcji wykładniczej). Funkcja jest rosnąca, dlatego najmniejsza wartość funkcji będzie w punkcie https://pandia.ru/text/80/379/images/image075_0.gif" width="145" height="29" > Punkty b) 
, V) 
d) samodzielnie rozwiązywać zeszyty, sprawdzimy to ustnie.
Uczniowie rozwiązują problem w zeszycie
|
Funkcja malejąca
|
Funkcja malejąca
|
Funkcja rosnąca
|
największa wartość funkcji w przedziale
najmniejsza wartość funkcji w przedziale
najmniejsza wartość funkcji w przedziale
największa wartość funkcji w przedziale- № 000. Znajdź największą i najmniejszą wartość danej funkcji w zadanym przedziale a) 
. To zadanie jest prawie takie samo jak poprzednie. Ale tutaj nie podano segmentu, ale promień. Wiemy, że funkcja jest rosnąca i nie ma ani największej, ani najmniejszej wartości na całej osi liczbowej https://pandia.ru/text/80/379/images/image063_0.gif" width="68" height = „20”>, i dąży do , tj. na promieniu funkcja at dąży do 0, ale nie ma własnego najmniejsza wartość, ale ma największą wartość w punkcie 
. Punkty b) 
, V) 
, G) 
Rozwiążcie własne zeszyty, sprawdzimy to ustnie.
Najpierw wprowadzimy definicję funkcji wykładniczej.
Funkcja wykładnicza $f\left(x\right)=a^x$, gdzie $a >1$.
Wprowadźmy własności funkcji wykładniczej dla $a >1$.
\ \[bez korzeni\] \
Przecięcie z osiami współrzędnych. Funkcja nie przecina osi $Ox$, ale przecina oś $Oy$ w punkcie $(0,1)$.
$f""\left(x\right)=(\left(a^xlna\right))"=a^x(ln)^2a$
\ \[bez korzeni\] \
Wykres (ryc. 1).
Rysunek 1. Wykres funkcji $f\left(x\right)=a^x,\ for \ a >1$.
Funkcja wykładnicza $f\left(x\right)=a^x$, gdzie $0
Wprowadźmy własności funkcji wykładniczej dla $0
Dziedziną definicji są wszystkie liczby rzeczywiste.
$f\left(-x\right)=a^(-x)=\frac(1)(a^x)$ -- funkcja nie jest ani parzysta, ani nieparzysta.
$f(x)$ jest ciągła w całej dziedzinie definicji.
Zakres wartości to przedział $(0,+\infty)$.
$f"(x)=\left(a^x\right)"=a^xlna$
\ \[bez korzeni\] \ \[bez korzeni\] \
Funkcja jest wypukła na całej dziedzinie definicji.
Zachowanie na końcach zakresu:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=+\infty \] \[(\mathop(lim)_(x\to +\infty ) a^x\ ) =0\]
Wykres (ryc. 2).
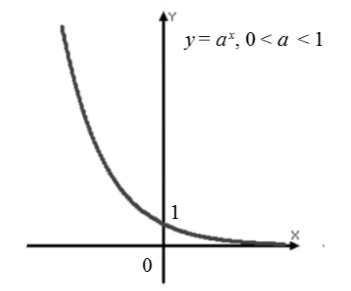
Przykład zadania konstruowania funkcji wykładniczej
Zbadaj i wykreśl funkcję $y=2^x+3$.
Rozwiązanie.
Zróbmy badanie na przykładzie powyższego schematu:
Dziedziną definicji są wszystkie liczby rzeczywiste.
$f\left(-x\right)=2^(-x)+3$ -- funkcja nie jest ani parzysta, ani nieparzysta.
$f(x)$ jest ciągła w całej dziedzinie definicji.
Zakres wartości to przedział $(3,+\infty)$.
$f"\left(x\right)=(\left(2^x+3\right))"=2^xln2>0$
Funkcja rośnie w całej dziedzinie definicji.
$f(x)\ge 0$ w całej dziedzinie definicji.
Przecięcie z osiami współrzędnych. Funkcja nie przecina osi $Ox$, ale przecina oś $Oy$ w punkcie ($0,4)$
$f""\left(x\right)=(\left(2^xln2\right))"=2^x(ln)^22>0$
Funkcja jest wypukła na całej dziedzinie definicji.
Zachowanie na końcach zakresu:
\[(\mathop(lim)_(x\to -\infty ) a^x\ )=0\] \[(\mathop(lim)_(x\to +\infty ) a^x\ )=+ \infty\]
Wykres (ryc. 3).
Rysunek 3. Wykres funkcji $f\left(x\right)=2^x+3$